Expert insights on synthetic data
The lastest
How test data generators support compliance and data privacy
Whether you’re generating data from scratch or transforming sensitive production data, performant test data generators are critical tools for achieving compliance in development workflows.

Blog posts
Thank you! Your submission has been received!
Oops! Something went wrong while submitting the form.
Test data management
Data privacy
Tonic Structural
Tonic Textual
Tonic Fabricate
Data de-identification
Data privacy
Product updates
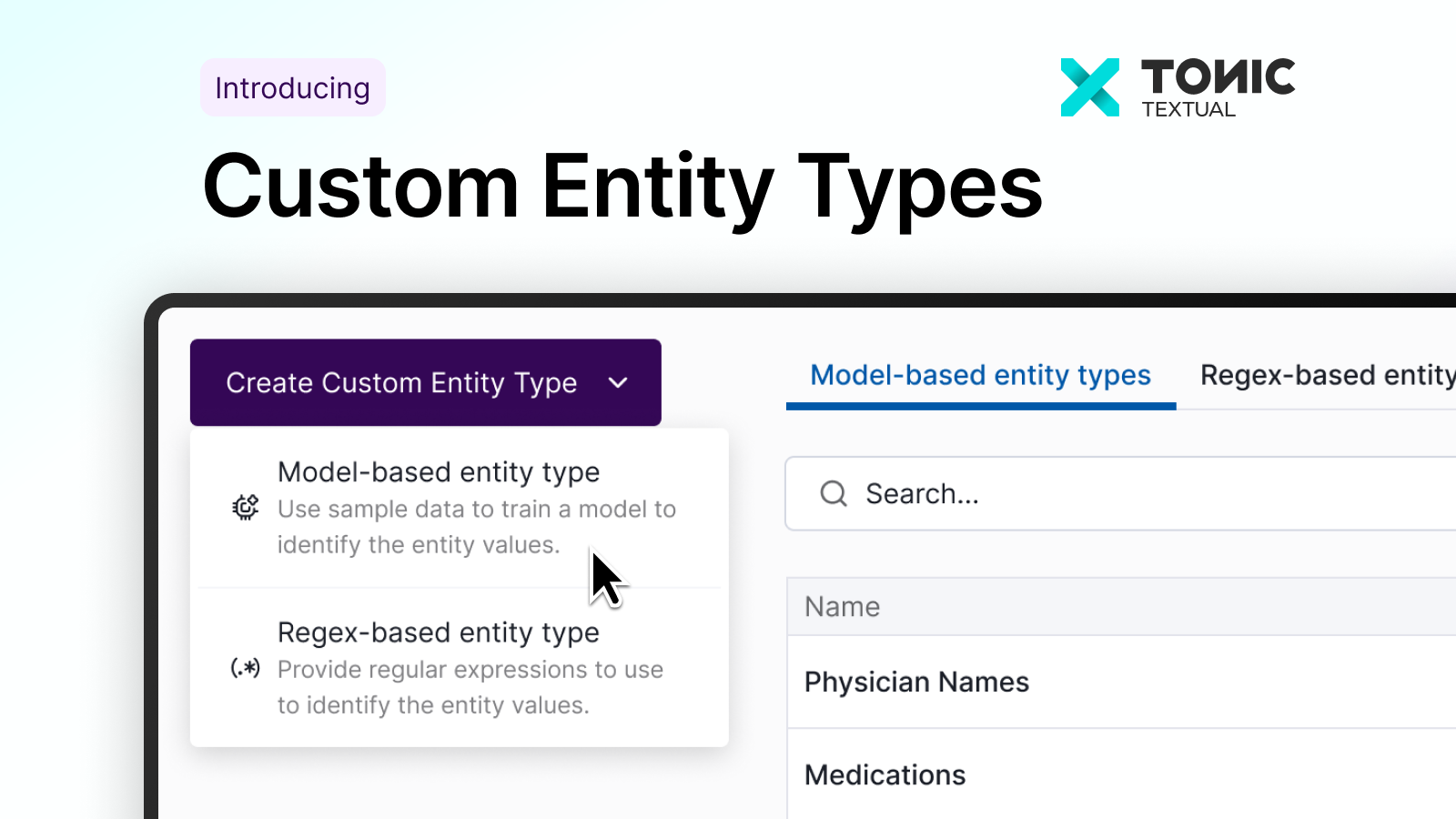
Tonic Textual

Hyper-realistic synthetic data via agentic AI has arrived. Meet the Fabricate Data Agent.
Product updates
Product updates
Generative AI
Tonic.ai editorial
Data synthesis
Tonic Fabricate
Product updates
Generative AI
Data privacy
Tonic Textual
Product updates
Tonic.ai editorial
Tonic Fabricate
Tonic Structural
Tonic Textual
Data privacy
Generative AI
Tonic Textual
Generative AI
Data privacy
Tonic Structural
Tonic Textual
Tonic Fabricate
Product updates
Tonic Structural
Tonic Textual
Tonic Fabricate

.svg)
.svg)




















.svg)